如何用度规表达克氏符？《张朝阳的物理课》再论克氏符

在往期的课程中，张朝阳用对偶基矢直观地解释了很多微分几何的概念，例如克氏符描述的是下基矢的坐标偏导对上基矢的内积。然而在实际计算中，基矢的坐标偏导并不是一个容易直接计算的量，所以往往采用的是求度规的坐标偏导的计算公式。那为什么对度规求偏导可以给出克氏符呢？

3月25日12时，《张朝阳的物理课》第二百四十一期开播，搜狐创始人、董事局主席兼CEO、物理学博士张朝阳坐镇搜狐视频直播间，为观众解答这一疑问。本节课首先回顾了张量分析中对偶基矢的定义以及逆变指标和协变指标的含义，然后通过用对偶基矢定义了度规和克氏符，并证明了这样的度规具有升降指标功能，最后推导出克氏符的度规表达式，与教科书上的计算公式一致，且更具有直观的几何含义。

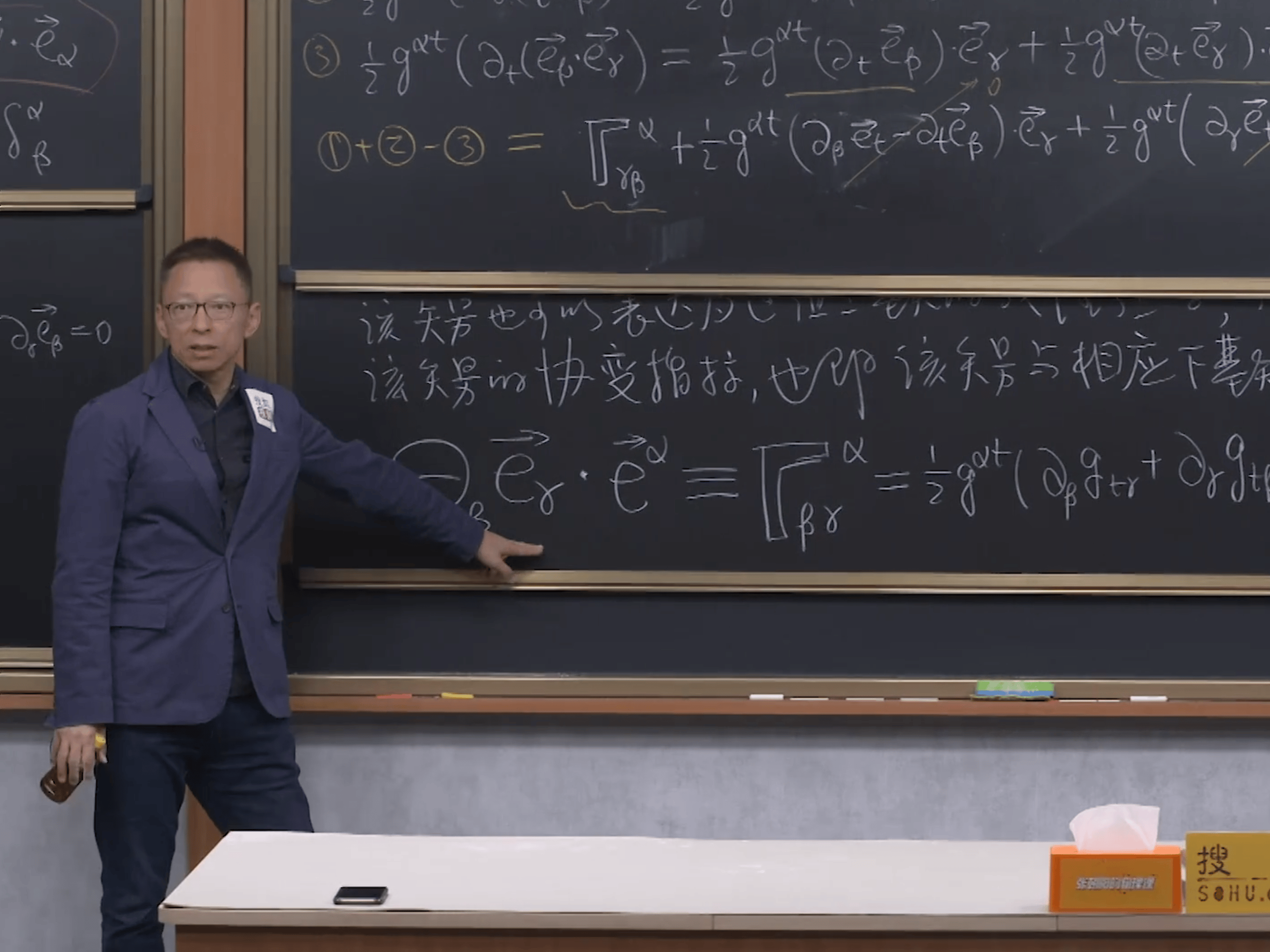
对偶基矢和度规

对于一个线性空间，无论它的维数是多少，人们总可以找到一组线性无关的基矢e_α，将其中的任意矢量V表示成

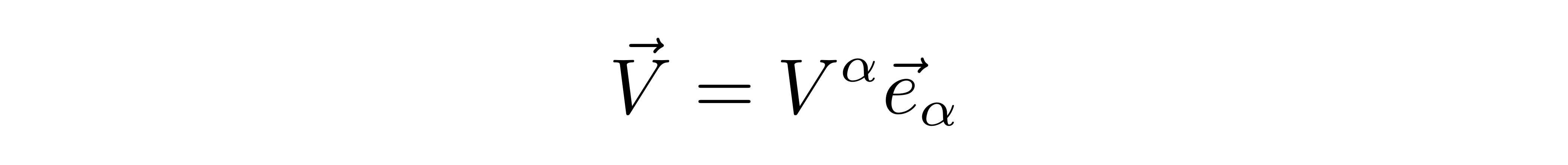
其中α的数量就是空间的维度，V^α称为矢量V的逆变分量。由于我们把α指标写在基矢e的下边，因此称这组基矢为下基矢。与此同时，我们还可以在这个空间里找到另外一组基矢，我们用带有上指标的符号e^β来表示，称为上基矢。由于下基矢是线性无关的，所以总可以找到与之对偶的上基矢。所谓对偶，指的是上下基矢满足

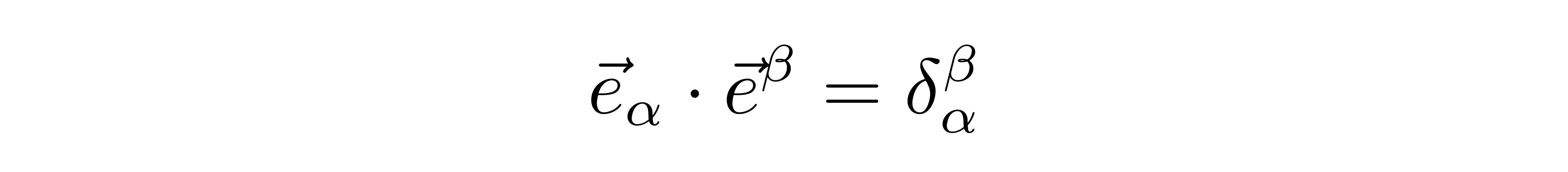
有了这样一组上基矢后，我们还可以把矢量表示成